Hello,
Après avoir débuté la lecture de Machine Learning avec Scikit-Learn, j’ai pris au mot l’auteur dès la fin du deuxième chapitre et j’ai tenté d’appliquer la méthode sur des données “réelles”.
J’ai donc été sur le site Kaggle qui propose (entre autre) un jeu de données pour débutant autour du Titanic, le but est de prédire les survivants. Bon, on se retrousse les manches, c’est parti !
Découverte des données
Récupération des informations
L’ensemble des données est fourni dans deux fichiers CSV : train.csv pour nous permettre d’entrainer un modèle et test.csv qui nous permettra de valider (ou non) notre algorithme.
La librairie Pandas nous permet facilement de charger des fichiers CSV :
import pandas as pd
titanic = pd.read_csv('train.csv')
Regardons ce que contient notre fichier :
titanic.head()
| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th… | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 4 | 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
Les données semblent cohérentes, regardons cela un peu plus en détails.
Description des données
On utilise la fonction info qui nous donne un résumé des différentes variables :
titanic.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 891 entries, 0 to 890
Data columns (total 12 columns):
PassengerId 891 non-null int64
Survived 891 non-null int64
Pclass 891 non-null int64
Name 891 non-null object
Sex 891 non-null object
Age 714 non-null float64
SibSp 891 non-null int64
Parch 891 non-null int64
Ticket 891 non-null object
Fare 891 non-null float64
Cabin 204 non-null object
Embarked 889 non-null object
dtypes: float64(2), int64(5), object(5)
memory usage: 83.6+ KB
Chaque valeur représente :
- PassengerID : un numéro d’identifiant
- Survived : 0 si ce passager n’a pas survécu, 1 dans le cas contraire
- Pclass : la classe dans laquelle ce passager a voyagé (1, 2 ou 3)
- Name : le nom
- Sex : femme ou homme (male ou female)
- Age : l’âge (en années)
- SibSp : le nombre de frère, soeur et/ou épouse à bord
- Parch : le nombre de parent et/ou d’enfant à bord
- Ticket : numéro du ticket
- Fare : prix du billet
- Cabin : numéro de cabine
- Embarked : port d’embarquement(C = Cherbourg, Q = Queenstown, S = Southampton)
Il y a quelques valeurs qui ne sont pas numériques (Name, Sex, Ticket, Cabin et Embarked). Il faut donc soit s’en séparer, soit les convertir. Ici, je pense me séparer de toutes (ce choix est tout à fait arbitraire, j’estime que ces données ne sont pas pertinentes pour déterminer si oui ou non ce passager survivra) sauf la variable Sex que je vais convertir (plus loin) en une variable binaire (0 ou 1), en associant par exemple female=0 et male=1.
Edit : au final, ca sera un peu différent avec une colonne pour male (valeur à 1 si c’est un homme, 0 sinon) et une autre pour female avec le même principe.
Il y a également un autre problème. Il y a 891 passagers répertoriés mais pour la variable Age, il n’y a que 714 valeurs. Il va falloir trouver une solution pour remplir les données manquantes car les algorithmes de machine learning (ML) ne peuvent pas travailler sur des données vides.
Examinons un peu plus nos données avec la fonction describe qui nous donne un petit tableau récapitulatif de quelques données statistiques de base :
titanic.describe()
| PassengerId | Survived | Pclass | Age | SibSp | Parch | Fare | |
|---|---|---|---|---|---|---|---|
| count | 891.000000 | 891.000000 | 891.000000 | 714.000000 | 891.000000 | 891.000000 | 891.000000 |
| mean | 446.000000 | 0.383838 | 2.308642 | 29.699118 | 0.523008 | 0.381594 | 32.204208 |
| std | 257.353842 | 0.486592 | 0.836071 | 14.526497 | 1.102743 | 0.806057 | 49.693429 |
| min | 1.000000 | 0.000000 | 1.000000 | 0.420000 | 0.000000 | 0.000000 | 0.000000 |
| 25% | 223.500000 | 0.000000 | 2.000000 | 20.125000 | 0.000000 | 0.000000 | 7.910400 |
| 50% | 446.000000 | 0.000000 | 3.000000 | 28.000000 | 0.000000 | 0.000000 | 14.454200 |
| 75% | 668.500000 | 1.000000 | 3.000000 | 38.000000 | 1.000000 | 0.000000 | 31.000000 |
| max | 891.000000 | 1.000000 | 3.000000 | 80.000000 | 8.000000 | 6.000000 | 512.329200 |
On remarque tout d’abord que la fonction élimine toutes les variables non-numériques.
Autre point, pour Fare, il semble y avoir une valeur maximale très forte (512,3292) au regard de la moyenne (mean) qui est de 32,204. Il faudra donc voir s’il s’agit d’une fausse valeur et si oui, comment on la traite (élimination de celle-ci, remplacement par la moyenne ?).
Histogrammes des données
Pour avoir une vision graphique des valeurs, nous allons utiliser la librairie Matplotlib pour afficher les histogrammes des valeurs numériques :
# chargement de la librairie dans un notebook Jupyter
%matplotlib inline
import matplotlib.pyplot as plt
titanic.hist(bins=50, figsize=(20,15))
plt.show()
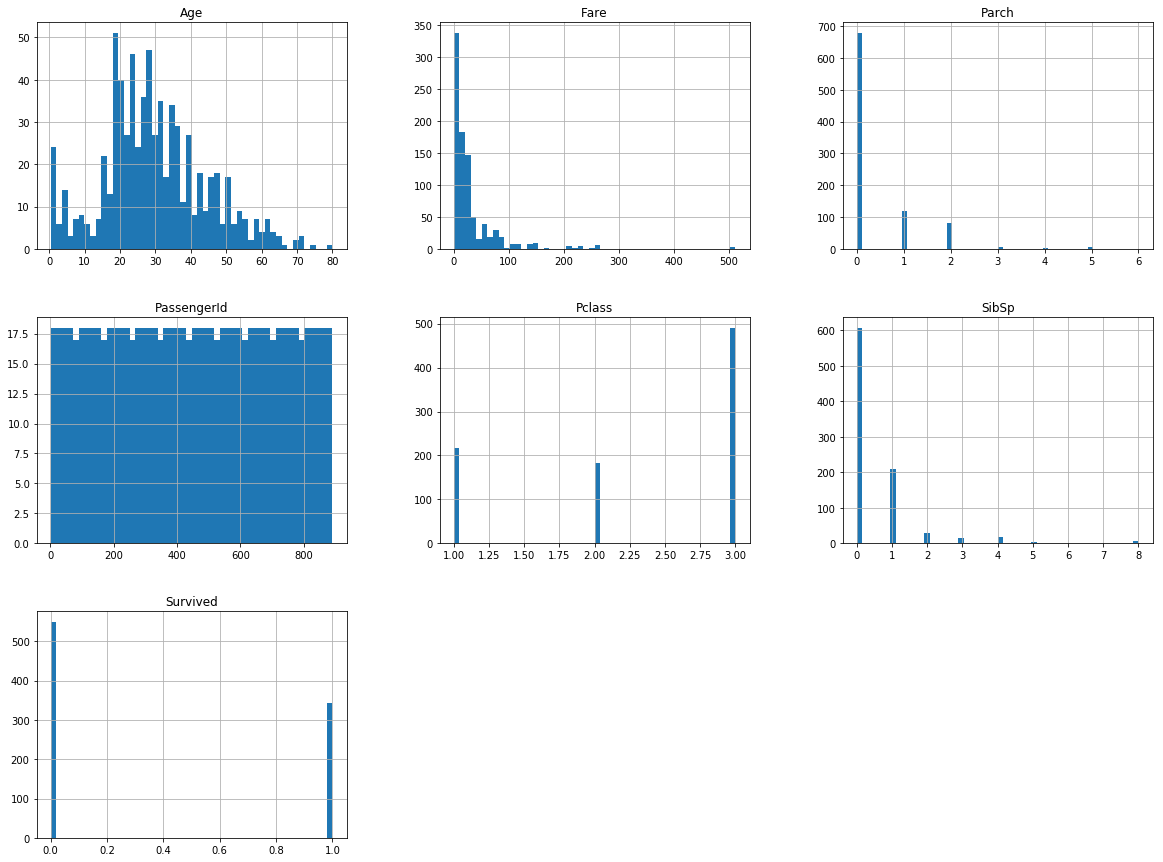
Quelques remarques sur ces graphiques
- Les âges semblent répartis à peu près de façon gaussienne, on notera toutefois le pic de valeur vers 0 : s’agit-il d’une valeur par défaut ou il y un forte proportion de nouveaux nés dans nos données ?
- Concernant les tarifs (Fare), on constate de nouveau un pic très important au tout début, ce qui semble écraser les autres valeurs.
- Il y a une forme de similarité entre Parch et SibSp, il y a peut-être une possibilité de simplifier ces valeurs ?
Pour essayer de répondre à la question 1, utilisons la fonction sort_values à laquelle on va lui demander de nous trier les données selon l’âge (paramètre by=), dans l’ordre croissant (paramètre ascending=True) et seulement les 10 premières valeurs ([:10], fonctionne comme le slicing Python) :
titanic.sort_values(by=['Age'], ascending=True)[:10]
| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 803 | 804 | 1 | 3 | Thomas, Master. Assad Alexander | male | 0.42 | 0 | 1 | 2625 | 8.5167 | NaN | C |
| 755 | 756 | 1 | 2 | Hamalainen, Master. Viljo | male | 0.67 | 1 | 1 | 250649 | 14.5000 | NaN | S |
| 644 | 645 | 1 | 3 | Baclini, Miss. Eugenie | female | 0.75 | 2 | 1 | 2666 | 19.2583 | NaN | C |
| 469 | 470 | 1 | 3 | Baclini, Miss. Helene Barbara | female | 0.75 | 2 | 1 | 2666 | 19.2583 | NaN | C |
| 78 | 79 | 1 | 2 | Caldwell, Master. Alden Gates | male | 0.83 | 0 | 2 | 248738 | 29.0000 | NaN | S |
| 831 | 832 | 1 | 2 | Richards, Master. George Sibley | male | 0.83 | 1 | 1 | 29106 | 18.7500 | NaN | S |
| 305 | 306 | 1 | 1 | Allison, Master. Hudson Trevor | male | 0.92 | 1 | 2 | 113781 | 151.5500 | C22 C26 | S |
| 827 | 828 | 1 | 2 | Mallet, Master. Andre | male | 1.00 | 0 | 2 | S.C./PARIS 2079 | 37.0042 | NaN | C |
| 381 | 382 | 1 | 3 | Nakid, Miss. Maria (“Mary”) | female | 1.00 | 0 | 2 | 2653 | 15.7417 | NaN | C |
| 164 | 165 | 0 | 3 | Panula, Master. Eino Viljami | male | 1.00 | 4 | 1 | 3101295 | 39.6875 | NaN | S |
Tout compte fait, il n’y a pas d’incohérence, juste une forte proportion de nouveaux nés à bord.
Dans le même ordre d’idée, regardons les données sur le tarif des billets :
titanic.sort_values(by=['Fare'], ascending=False)[:10]
| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 258 | 259 | 1 | 1 | Ward, Miss. Anna | female | 35.0 | 0 | 0 | PC 17755 | 512.3292 | NaN | C |
| 737 | 738 | 1 | 1 | Lesurer, Mr. Gustave J | male | 35.0 | 0 | 0 | PC 17755 | 512.3292 | B101 | C |
| 679 | 680 | 1 | 1 | Cardeza, Mr. Thomas Drake Martinez | male | 36.0 | 0 | 1 | PC 17755 | 512.3292 | B51 B53 B55 | C |
| 88 | 89 | 1 | 1 | Fortune, Miss. Mabel Helen | female | 23.0 | 3 | 2 | 19950 | 263.0000 | C23 C25 C27 | S |
| 27 | 28 | 0 | 1 | Fortune, Mr. Charles Alexander | male | 19.0 | 3 | 2 | 19950 | 263.0000 | C23 C25 C27 | S |
| 341 | 342 | 1 | 1 | Fortune, Miss. Alice Elizabeth | female | 24.0 | 3 | 2 | 19950 | 263.0000 | C23 C25 C27 | S |
| 438 | 439 | 0 | 1 | Fortune, Mr. Mark | male | 64.0 | 1 | 4 | 19950 | 263.0000 | C23 C25 C27 | S |
| 311 | 312 | 1 | 1 | Ryerson, Miss. Emily Borie | female | 18.0 | 2 | 2 | PC 17608 | 262.3750 | B57 B59 B63 B66 | C |
| 742 | 743 | 1 | 1 | Ryerson, Miss. Susan Parker “Suzette” | female | 21.0 | 2 | 2 | PC 17608 | 262.3750 | B57 B59 B63 B66 | C |
| 118 | 119 | 0 | 1 | Baxter, Mr. Quigg Edmond | male | 24.0 | 0 | 1 | PC 17558 | 247.5208 | B58 B60 | C |
Finalement, c’est cohérent : les tarifs les plus élevés sont ceux des passagers de la première classe.
Passons à l’étape suivante !
Recherche de corrélations
Le but est ici de voir s’il n’existe pas de corrélations entre différentes valeurs. On utilise pour cela la fonction corr :
titanic.corr()
| PassengerId | Survived | Pclass | Age | SibSp | Parch | Fare | |
|---|---|---|---|---|---|---|---|
| PassengerId | 1.000000 | -0.005007 | -0.035144 | 0.036847 | -0.057527 | -0.001652 | 0.012658 |
| Survived | -0.005007 | 1.000000 | -0.338481 | -0.077221 | -0.035322 | 0.081629 | 0.257307 |
| Pclass | -0.035144 | -0.338481 | 1.000000 | -0.369226 | 0.083081 | 0.018443 | -0.549500 |
| Age | 0.036847 | -0.077221 | -0.369226 | 1.000000 | -0.308247 | -0.189119 | 0.096067 |
| SibSp | -0.057527 | -0.035322 | 0.083081 | -0.308247 | 1.000000 | 0.414838 | 0.159651 |
| Parch | -0.001652 | 0.081629 | 0.018443 | -0.189119 | 0.414838 | 1.000000 | 0.216225 |
| Fare | 0.012658 | 0.257307 | -0.549500 | 0.096067 | 0.159651 | 0.216225 | 1.000000 |
On va s’intéresser principalement à la colonne Survived puisqu’il s’agit de notre variable à expliquer. Il y un coefficient de corrélation qui semble intéressant avec Pclass (-0,33), Fare (0,25) et peut-être avec Parch ou Age. Pour regarder cela graphiquement, on utilise la fonction scatter_matrix du module plotting de Pandas :
from pandas.plotting import scatter_matrix
attrs = ['Pclass', 'Fare', 'Parch', 'Age']
scatter_matrix(titanic[attrs], figsize=(12,8))
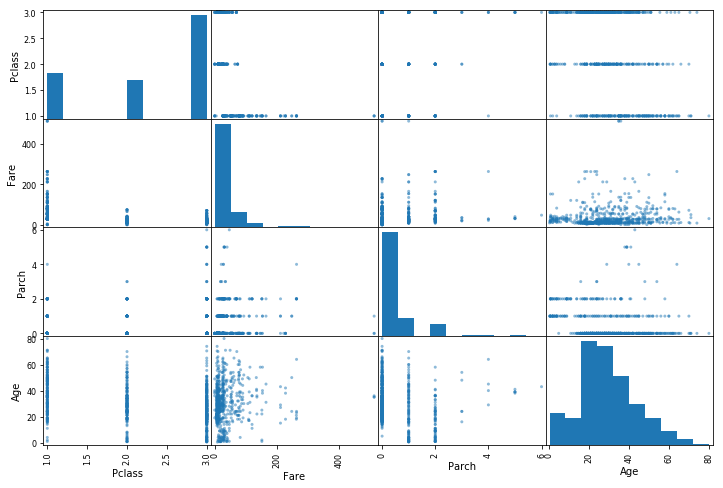
Bon, décevant :(. La colonne Pclass contient que des 1, 2 ou 3, ce qui rassemble les données sur 3 colonnes. A ce stade, je n’en déduit rien qui puisse m’aider à prédire si oui ou non cette personne survivra.
Il est de temps de passer à la préparation des données afin de pouvoir automatiser tout le processus. Ceci permet dans le cas où des nouvelles données apparaissent, de les mettre directement en forme pour l’algorithme.
Préparation des données
Puisque nous allons utiliser un algorithme d’apprentissage supervisé (puisque nous connaissons les valeurs à obtenir), il nous faut séparer les labels (la réponse attendu en fait) des données :
labels = titanic["Survived"]
Il faut maintenant préparer les données selon nos observations précédentes, c’est à dire :
- retirer les colonnes Name, Ticket, Cabin, Embarked, et PassengerId qui ne nous sert à rien pour la prédiction; on retire également Survived puisque nous avons récupérer les étiquettes,
- coder en binaire s’il s’agit de femme ou d’homme,
- remplir les valeurs d’âge manquantes,
- étape supplémentaire : recalibrer les données (on en parlera plus loin).
Retirer des colonnes
On utilise la fonction drop qui renvoi un Dataframe sans les colonnes voulues :
data_without_columns = titanic.drop(["Name", "Ticket", "Cabin", "Embarked", "PassengerId", "Survived"], axis=1)
Encoder une variable en binaire
La librairie Scikit-Learn possède une fonction LabelBinarizer dans son module de pré-traitement qui permet de réaliser directement cet encodage. Mais le retour de cette fonction un tableau Numpy qu’il faut donc réinjecter dans un Dataframe de Pandas.
Or Pandas permet également de réaliser cet encodage avec sa fonction get_dummies :
data_binarized = pd.get_dummies(data_without_columns, columns=["Sex"])
Valeurs d’âge manquantes
Scikit-Learn permet de facilement gérer les données manquantes à l’aide de la fonction imputer. Il suffit de l’instancier avec la stratégie voulue puis appliquer les données à l’instance de classe créée. Elle retourne un tableau Numpy qu’il faut remettre dans un Dataframe de Pandas.
Voici comment ça fonctionne :
from sklearn.preprocessing import Imputer
imputer = Imputer(strategy="median")
X = imputer.fit_transform(data_binarized)
# reinject in pandas.Dataframe:
data_median = pd.DataFrame(X, columns=data_binarized.columns)
Jetons un coup d’oeil à nos données :
data_median.info()
<class ‘pandas.core.frame.DataFrame’> RangeIndex: 891 entries, 0 to 890 Data columns (total 7 columns): Pclass 891 non-null float64 Age 891 non-null float64 SibSp 891 non-null float64 Parch 891 non-null float64 Fare 891 non-null float64 Sex_female 891 non-null float64 Sex_male 891 non-null float64 dtypes: float64(7) memory usage: 48.8 KB
C’est plutôt satisfaisant ! Attaquons-nous maintenant à la recalibration des données : j’utilise ici la standardization (in english, en français la normalisation) qui permet de mettre toutes les valeurs à la même échelle, afin de respecter les contraintes des algorithmes.
Scikit-Learn propose un transformateur pour cela : StandardScaler du module preprocessing. Comme les autres fonctions, le retour est un tableau Numpy, que l’on remet sous le format pd.Dataframe :
from sklearn.preprocessing import StandardScaler
std = StandardScaler()
X = std.fit_transform(data_median)
data_std = pd.DataFrame(X, columns=data_median.columns)
data_std.head()
| Pclass | Age | SibSp | Parch | Fare | Sex_female | Sex_male | |
|---|---|---|---|---|---|---|---|
| 0 | 0.827377 | -0.565736 | 0.432793 | -0.473674 | -0.502445 | -0.737695 | 0.737695 |
| 1 | -1.566107 | 0.663861 | 0.432793 | -0.473674 | 0.786845 | 1.355574 | -1.355574 |
| 2 | 0.827377 | -0.258337 | -0.474545 | -0.473674 | -0.488854 | 1.355574 | -1.355574 |
| 3 | -1.566107 | 0.433312 | 0.432793 | -0.473674 | 0.420730 | 1.355574 | -1.355574 |
| 4 | 0.827377 | 0.433312 | -0.474545 | -0.473674 | -0.486337 | -0.737695 | 0.737695 |
Nos données sont maintenant prêtes à être fournies aux algorithmes de machine learning ; elles ne ressemblent plus vraiment aux données d’origine (cf le résultat de la fonction head ci-dessus) mais elles sont conformes à ce qu’attendent ces algorithmes.
Note sur la partie “Préparation des données”
L’état de l’art aurait voulu que j’utilise des Pipeline afin de réaliser la préparation des données et permettre l’automatisation de cette tâche. Je ne l’ai pas fait içi pour principalement deux raisons :
- Je découvre le machine learning et j’applique pas à pas la méthode du livre cité au début de l’article : chaque chose en son temps (même si les Pipeline y sont expliqués).
- Je n’aurais pas de nouvelles données et je ne mettrais donc pas en production le résultat de cette étude.
Mais dans un cadre réel, il faudra automatiser toute cette partie afin de mettre à jour facilement les données afin d’augmenter la performance de l’algorithme choisi.
Choix et entrainement d’un modèle
Pour mémoire, nos données sont dans la variable data_std et les étiquettes dans labels. La librairie Scikit-Learn nous donne un certain nombre de modèle, nous allons donc tester nos valeurs sur certains d’entre-eux :
LinearRegression
Pour utiliser la régression linéaire, il suffit d’instancier le modèle LinearRegression puis de l’entrainer avec nos valeurs comme ceci :
from sklearn.linear_model import LinearRegression
linreg = LinearRegression()
linreg.fit(data_std, labels)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
Score
Il nous faut maintenant évaluer nos résultats. Pour ce faire, j’utilise la validation croisée en K passes en appliquant la fonction cross_val_score du module model_selection. Cette fonction permet de découper aléatoirement le jeu d’entrainement en K morceaux, ce qui permet de faire plus d’entrainement (au nombre de K).
import numpy as np
from sklearn.model_selection import cross_val_score
linreg_score = cross_val_score(linreg, data_std, labels, scoring="neg_mean_squared_error", cv=10)
linreg_rmse = np.sqrt(-linreg_score)
print(linreg_rmse)
print("Moyenne", linreg_rmse.mean())
print("Ecart-type", linreg_rmse.std())
[ 0.38779897 0.37348749 0.39836752 0.39084261 0.38957355 0.37855029 0.39663624 0.40125233 0.32840724 0.37762877] Moyenne 0.382254499421 Ecart-type 0.0199923822969
On obtient une moyenne de la racine carrée de l’erreur quadratique moyenne (RMSE) de 0.38 ; nous, nous cherchons à obtenir une valeur d’erreur la plus petite possible
Essayons avec un autre algorithme :
DecisionTreeRegressor
Même chose avec le modèle DecisionTreeRegressor :
from sklearn.tree import DecisionTreeRegressor
treereg = DecisionTreeRegressor()
treereg.fit(data_std, labels)
DecisionTreeRegressor(criterion='mse', max_depth=None, max_features=None,
max_leaf_nodes=None, min_impurity_decrease=0.0,
min_impurity_split=None, min_samples_leaf=1,
min_samples_split=2, min_weight_fraction_leaf=0.0,
presort=False, random_state=None, splitter='best')
On notera ici la présence de nombreux hyperparamètres, chacun peut permettre d’affiner le résultat obtenu. Ces hyperparamètres ne se règlent qu’une fois le bon modèle trouvé !
Score
De la même manière :
treereg_score = cross_val_score(treereg, data_std, labels, scoring="neg_mean_squared_error", cv=10)
treereg_rmse = np.sqrt(-treereg_score)
print(treereg_rmse)
print("Moyenne", treereg_rmse.mean())
print("Ecart-type", treereg_rmse.std())
[ 0.4868645 0.47942838 0.51979766 0.4747034 0.44699689 0.40609775 0.45067181 0.50280114 0.43673578 0.39404905] Moyenne 0.45981463686 Ecart-type 0.0384382715703
Ah ! C’est encore moins bien ! Essayons un autre :
RandomForestRegressor
Nouvel essai avec RandomForestRegressor :
from sklearn.ensemble import RandomForestRegressor
forest = RandomForestRegressor()
forest.fit(data_std, labels)
RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=None,
max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=10, n_jobs=1,
oob_score=False, random_state=None, verbose=0, warm_start=False)
Score
Et de même :
forest_score = cross_val_score(forest, data_std, labels, scoring="neg_mean_squared_error", cv=10)
forest_rmse = np.sqrt(-forest_score)
print(forest_rmse)
print("Moyenne", forest_rmse.mean())
print("Ecart-type", forest_rmse.std())
[ 0.45047666 0.39228221 0.44474933 0.36923691 0.35309265 0.36961988 0.4282808 0.41886481 0.34147062 0.33537571] Moyenne 0.390344958784 Ecart-type 0.0406264102691
C’est à peine mieux qu’une régression linéaire…
Affiner son modèle
Maintenant que nous avons testé 3 modèles différents, nous pouvons tenter d’en améliorer un (je choisis ici le dernier, le RandomForestRegressor) en optimisant ses hyperparamètres. On va donc effectuer une recherche aléatoire par quadrillage sur quelques paramètres en utilisant la fonction RandomizedSearchCV :
%%time
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import randint
param_dist = {"n_estimators": randint(20, 50),
"max_features": randint(2, 8),
"bootstrap": [True]}
forest = RandomForestRegressor()
grid = RandomizedSearchCV(forest, param_dist, cv=20, scoring="neg_mean_squared_error")
grid.fit(data_std, labels)
CPU times: user 20.5 s, sys: 99.9 ms, total: 20.6 s Wall time: 20.7 s
%%time permet d’afficher le temps d’exécution d’une cellule dans un notebook de Jupyter. Ici, presque 18 secondes sur ma machine pour tester 20 (cv=) combinaisons.
On maintenant affiche les meilleurs paramètres trouvés :
print(grid.best_estimator_)
print("Score : ", np.sqrt(-grid.best_score_))
RandomForestRegressor(bootstrap=True, criterion=‘mse’, max_depth=None, max_features=3, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, min_samples_leaf=1, min_samples_split=2, min_weight_fraction_leaf=0.0, n_estimators=45, n_jobs=1, oob_score=False, random_state=None, verbose=0, warm_start=False) Score : 0.370268736285
On améliore un peu le résultat final ! C’est plutôt bien, sachant que l’on joue ici que sur 3 paramètres. On obtient un score au final meilleur que la régression linéaire testée en premier.
Conclusion
Voilà, c’est fini pour ce premier essai en machine learning, avec des données réelles. Même si le résultat final n’est pas hyper précis, j’ai quand même appris plusieurs choses :
- la préparation des données est une tâche à part entière, qui occupe une bonne part de l’analyse,
- après deux chapitres, j’en ai appris beaucoup sur le l’apprentissage automatique, ce qui me met l’eau à la bouche pour la suite de ce livre (pour mémoire : Machine Learning avec Scikit-Learn),
- j’ai finalement apprécié de travailler dans un notebook de Jupyter, il y a pas mal de fonctionnalités intéressantes lorsque l’on fait du pas-à-pas avec son code,
J’ai maintenant hâte de continuer pour mieux comprendre le fonctionnement des algorithmes et comment les choisirs en fonction des besoins.
A bientôt pour la suite :)